En un post anterior comenté que había comenzado a leer un libro sobre SciPy y NumPy. En los primeros capítulos encontré ejemplos simples de la utilización de SciPy. Hoy voy a mostrar el código de dos de ellos, para los cuales implementé sus respectivos gráficos. El primero es sobre ajustar una distribución de puntos con dos Gaussianas, y el segundo es sobre encontrar los puntos de intersección de dos curvas.

Como cada paso está comentado en el código, entonces no me voy a detener en las explicaciones. Es más para tener estos ejemplos como anotaciones cuando necesite hacer un cálculo simple y un gráfico modesto, nada más que eso :-)

Si no tenemos los paquetes necesarios, en Fedora los instalamos así:

# yum install numpy scipy python-matplotlib

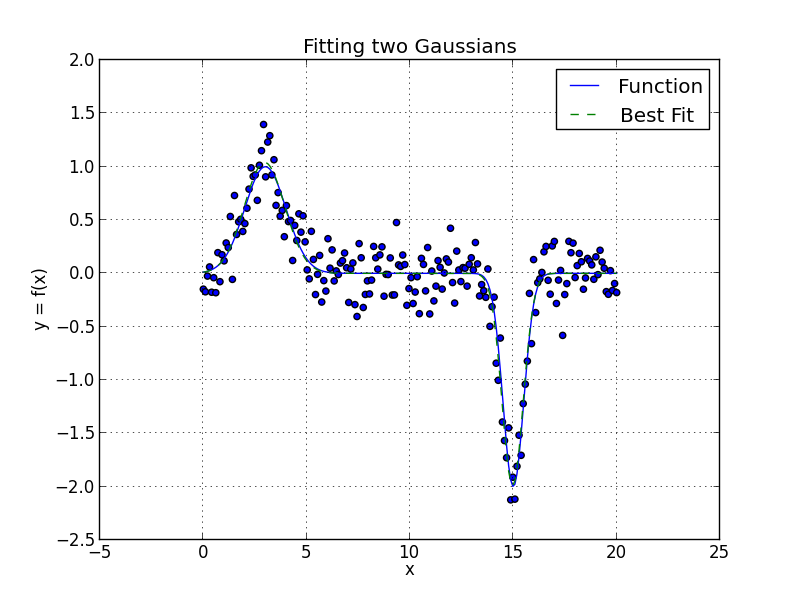
Ajuste de dos Gaussianas

Si usamos Vim, podemos usar el plugin para templates del cual hablábamos ayer. Entonces creamos el archivo:

$ vim fitting-two-gaussians.py

y copiamos el siguiente código:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# function to model and create data: Two-Gaussian
def func(x, a0, b0, c0, a1, b1, c1):
    return a0 * np.exp(-(x - b0)**2 / (2 * c0**2)) \
           + a1 * np.exp(-(x - b1)**2 / (2 * c1**2))

# clean data
x = np.linspace(0, 20, 200)
y = func(x, 1, 3, 1, -2, 15, 0.5)

# add noise to data
yn = y + 0.2 * np.random.normal(size=len(x))

# fit noisy data providing guesses
guesses = [1, 3, 1, 1, 15, 1]
popt, pcov = curve_fit(func, x, yn, p0=guesses)

# print best fit and variances (diagonal elements)
for i in range(0, 6):
    print "(", popt[i], "+/-", pcov[i,i], ")"

# plot
plt.title('Fitting two Gaussians')
plt.plot(x, y, label='Function')
plt.scatter(x, yn)
yfit = func(x, popt[0], popt[1], popt[2], popt[3], popt[4], popt[5])
plt.plot(x, yfit, '--', label='Best Fit')
plt.legend()
plt.xlabel('x')
plt.ylabel('y = f(x)')
plt.show()

Luego lo ejecutamos, pero antes le damos los permisos necesarios para ello:

$ chmod +x fitting-two-gaussians.py
$ ./fitting-two-gaussians.py
( 1.01566899098 +/- 0.00385041607346 )
( 3.01416857209 +/- 0.00491510905728 )
( 0.99386852028 +/- 0.00492078923246 )
( -1.91566245187 +/- 0.00722572741217 )
( 15.0208881795 +/- 0.000735898852204 )
( 0.529428527565 +/- 0.000735896650911 )

Como resultado, obtenemos los seis parámetros de las dos Gaussianas y sus respectivas incertezas. El gráfico es el siguiente (click para ampliar):

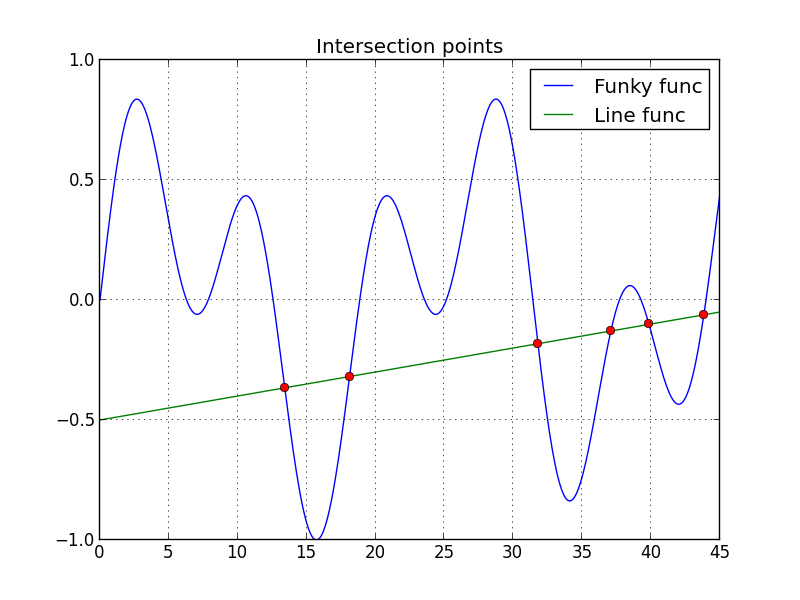
Intersección de dos curvas

Siguiendo los pasos anteriores, creamos el archivo:

$ vim intersection-points.py

y copiamos el siguiente código:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

# function to simplify intersection solution
def findIntersection(func1, func2, x0):
    return fsolve(lambda x: func1(x) - func2(x), x0)

# data range
x = np.linspace(0, 45, 10000)

# functions that will intersect
funky = lambda x: np.cos(x / 5) * np.sin(x / 2)
line = lambda x: 0.01 * x - 0.5

# starting estimate
x0 = [15, 20, 30, 35, 40, 45]

# solutions on intersection points
result = findIntersection(funky, line, x0)

for i in range(0, 6):
    print "(", result[i], ", ", line(result)[i], ")"

# plot
plt.title('Intersection points')
plt.plot(x, funky(x), label='Funky func')
plt.plot(x, line(x), label='Line func')
plt.plot(result, line(result), 'o')
plt.xlim(0, 45)
plt.ylim(-1, 1)
plt.legend()
plt.show()

Luego lo ejecutamos, dándole sus permisos antes:

$ chmod +x intersection-points.py
$ ./intersection-points.py
( 13.4077307829 ,  -0.365922692171 )
( 18.1136612829 ,  -0.318863387171 )
( 31.7833086315 ,  -0.182166913685 )
( 37.0799991955 ,  -0.129200008045 )
( 39.8483778612 ,  -0.101516221388 )
( 43.8258775032 ,  -0.0617412249676 )

En este caso, el resultado son los seis puntos de intersección entre las dos curvas. El gráfico es este (click para ampliar):